モンティ・ホール問題

ベイズ統計の本を最近読んでいるのだが、モンティ・ホール問題というのが書いてあった

 モンティ・ホール問題(Wikipedia)

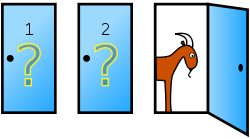
「プレーヤーの前に3つのドアがある。1つのドアの後ろに景品の新車が、残りドアの後ろには、はずれを意味するヤギがいる。プレーヤーが1つのドアを選択した後、番組司会者のモンティは、残りのドアのうちヤギがいるドアを開けてヤギを見せる。 ここでプレーヤーは、最初に選んだドアから、開いてないドアに変更してもよいと言われる。プレーヤーはドアを変更すべきだろうか？

 

最初に選んだドアの当たり確率＝1/3は、誰でもわかる

だけど、番組の司会者が、空いていないドアのうちヤギがいるものを開けた後、プレイヤーが自身の選択を変えるべきか？が問題なのだ 。

初めに考えた時、残りのドアが当たりの確率は1/2のような気がした。でも、たぶん、それだとクイズにならない。だからと言って、マシな答えも思い浮かばない。そこで、件のベイズ統計の本の答えを読んだのだが、意味が分からない

ということで、自分で、適当に考えてみた。僕は、司会者は当たりの場所を知っているけど、当たりドアは開けられない、という事実に注目してみた。

 (1)  最初に、プレーヤーの最初の選択＝当たりの時を考えてみる。 司会者は、残りのドアいずれかを開ける。ただ、開けるのはどっちでもよい、なぜならば、どっちもはずれだから。結局、プレーヤーがドアを変えると、はずれになる。

 (2) 次に、プレーヤーの最初の選択＝はずれを考えてみる。司会者は、残りの2つのドアのうち、必ずはずれを開く。なぜなら、当たりを開けたら、番組にならないから。すると、残りのドアが当たりになる。つまり、プレーヤーの最初の選択がはずれなら、移動したほうが良い。そして、プレーヤーがはずれを引くのは2パターンある

ただし、回答者は、自分の選択があたりなのか、はずれなのかはわからない。

がしかし、(1)と(2)を合わせると、都合3つの選択肢があることはわかる。そして、ドアを変えると、はずれるのが1コ、逆にドアを変えると当たるのが2コ。とすると、ドアを変えた時に当たる確率は2/3。最初の確率が1/3だったので、自分が当たっているかはわからないものの、ドアを変えたほうが良いというのが答え。

単純にこういうことのような気がするんだけど、違うんでしょうか？ ネット上の説明文よんでいても、なんだかピンときませんことよ、オホホ